[論文メモ] Unbiased Offline Recommender Evaluation for Missing-Not-At-Random Implicit Feedback

• 著者： Longqi Yang, Yin Cui, Yuan Xuan, Chenyang Wang, Serge Belongie, and Deborah Estrin
• 所属：Cornell University
• 発表会議：RecSys 2018

[link]

概要

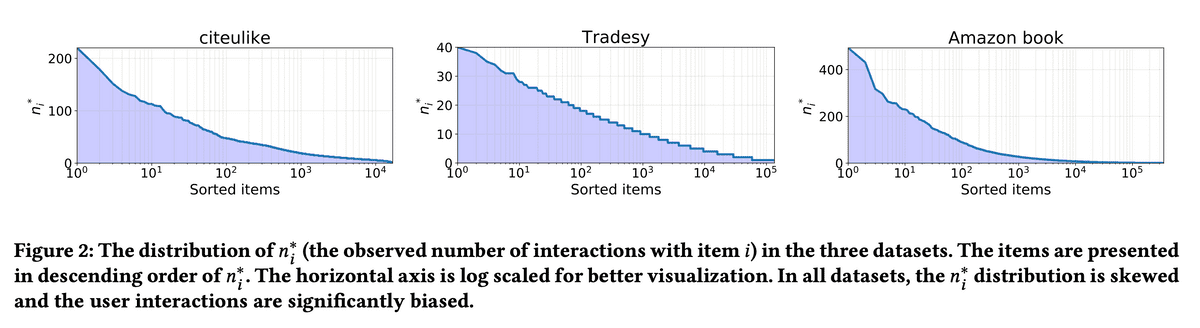
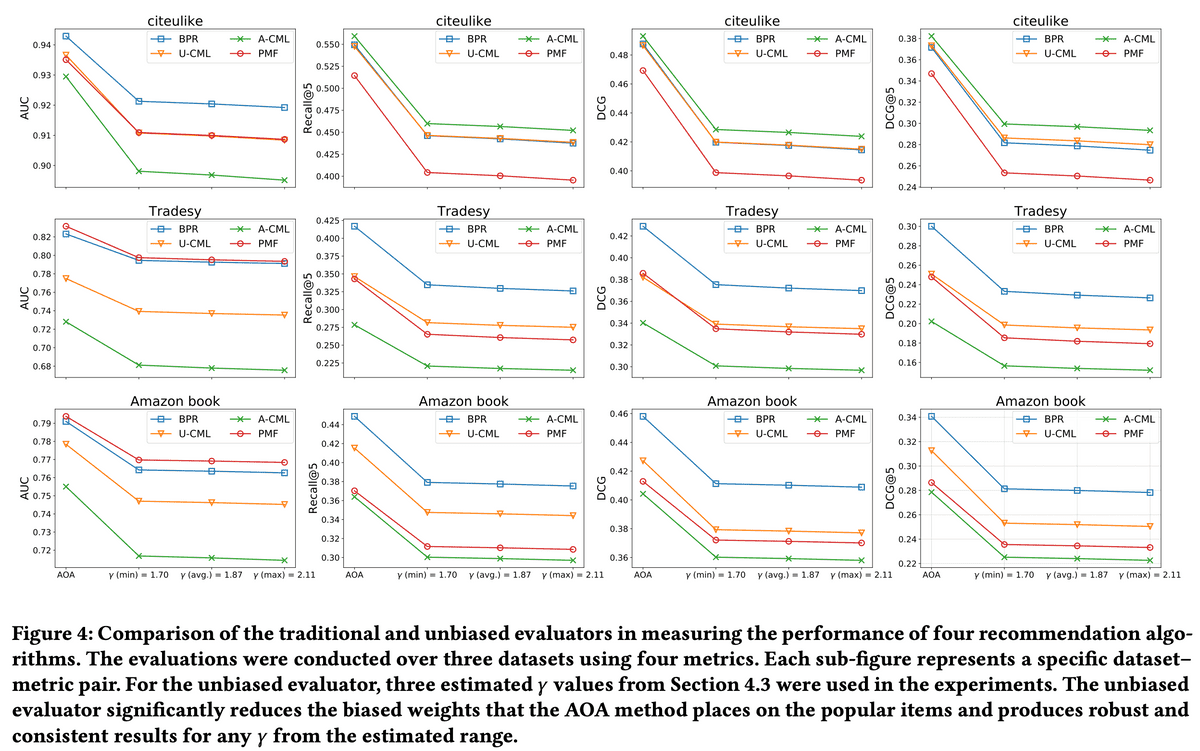
Implicit-feedback Recommendersにおいて、IPSを導入したUnbiased Evaluatorを提案。実験データはMNARであることを示し、Unbiased Evaluatorと従来のAverage-over-all (AOA) Evaluatorの結果を比較することでAOA Evaluatorが従来の推薦アルゴリズムの性能を過大評価していることを示唆した。

導入

Explicit FeedbackとImplicit Feedback

• Explicit Feedback

  • ユーザーからアイテムへの評価が陽に与えられている。(e.g. ★5)

• Implicit Feedback

  • ユーザーからアイテムへの評価が与えられず、クリックや購入の有無（0/1）しか与えられない。
  • Explicit Feedbackと比べて比較的容易に収集可能。
  • 今回の論文はこっち

(理想的な) Evaluatorについて

$R(\hat{Z})=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\left|\mathcal{S}_{u}\right|} \sum_{i \in \mathcal{S}_{u}} c\left(\hat{Z}_{u, i}\right)$

ここで $\hat{Z}_{u, i}$ はアイテム $i$ をユーザー $u$ に対して推薦する順位、 $\mathcal{S}_{u}$ はユーザー $u$ がpositive feedbackする全てのアイテム集合。AUCやDCGなどを計算したい場合、関数 $c$ を下記

にする、とあるがAUCの式はおかしい気が。。。

この理想的なEvaluatorはユーザーが全てのアイテムを認識しているわけではないのでそもそも $\mathcal{S}_{u} \subseteq \mathcal{I}$ が観測できない->計算できない。

(近似的な) Evaluatorについて

$\hat{R}_{\mathrm{AOA}}(\hat{Z})=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\left|\mathcal{S}_{u}^{*}\right|} \sum_{i \in \mathcal{S}_{u}^{*}} c\left(\hat{Z}_{u, i}\right)$

これをAverage-over-all (AOA) Evaluatorという。このとき、$\mathcal{S}_{u}$のうち観測できた集合を$\mathcal{S}_{u}^{*}$とする。 ユーザー$u$がアイテム$i$を観測した(1)か否か(0)を表す確率変数$O_{u, i}$を導入すると、

$\hat{R}_{\mathrm{AOA}}(\hat{Z})=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\sum_{i \in \mathcal{S}_{u}} O_{u, i}} \sum_{i \in \mathcal{S}_{u}} c\left(\hat{Z}_{u, i}\right) \cdot O_{u, i}$

と変形することができる。 しかしこれは

$\mathbb{E}_{O}\left[\hat{R}_{\mathrm{AOA}}(\hat{Z})\right] \neq R(\hat{Z})$

である。

提案手法

Unbiased Evaluator

AOA Evaluatorに対して傾向スコア(=ユーザー$u$がアイテム$i$にpositive feedbackする確率$P_{u,i}$)の逆数で重み付け(Inverse-Propensity-Scoring: IPS)を行う。直感的にはよく観測されるアイテムの重みは小さく、あまり観測されないアイテムの重みは大きくなるように重み付けを行う。

$\begin{aligned} \hat{R}_{\mathrm{IPS}}(\hat{Z} | P) &=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\left|\mathcal{S}_{u}\right|} \sum_{i \in \mathcal{S}_{u}^{*}} \frac{c\left(\hat{Z}_{u, i}\right)}{P_{u, i}} \\ &=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\left|\mathcal{S}_{u}\right|} \sum_{i \in \mathcal{S}_{u}} \frac{c\left(\hat{Z}_{u, i}\right)}{P_{u, i}} \cdot O_{u, i} \end{aligned}$

これについて期待値を取ると

$\begin{aligned} \mathbb{E}_{O}\left[\hat{R}_{\mathrm{IPS}}(\hat{Z} | P)\right] &=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\left|\mathcal{S}_{u}\right|} \sum_{i \in \mathcal{S}_{u}} \frac{c\left(\hat{Z}_{u, i}\right)}{P_{u, i}} \cdot \mathbb{E}_{O}\left[O_{u, i}\right] \\ &=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\left|\mathcal{S}_{u}\right|} \sum_{i \in \mathcal{S}_{u}} c\left(\hat{Z}_{u, i}\right)=R(\hat{Z}) \end{aligned}$

理想的なEvaluatorに一致することがわかる。 実際にはこのEvaluatorの分散を抑えるためにSelf-Normalized IPS (SNIPS)を導入する。

$\begin{aligned} \hat{R}_{\text {SNIPS }}(\hat{Z} | P) &=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\left|\mathcal{S}_{u}\right|} \frac{\mathbb{E}_{O}\left[\sum_{i \in \mathcal{S}_{u}^{*}} \frac{1}{P_{u, i}}\right]}{\sum_{i \in \mathcal{S}_{u}^{*}} \frac{1}{P_{u, i}}} \sum_{i \in \mathcal{S}_{u}^{*}} \frac{c\left(\hat{Z}_{u, i}\right)}{P_{u, i}} \\ &=\frac{1}{|\mathcal{U}|} \sum_{u \in \mathcal{U}} \frac{1}{\sum_{i \in \mathcal{S}_{u}^{*}} \frac{1}{P_{u, i}}} \sum_{i \in \mathcal{S}_{u}^{*}} \frac{c\left(\hat{Z}_{u, i}\right)}{P_{u, i}} \end{aligned}$

SNIPSの出典は下記参照。

• The Self-Normalized Estimator for Counterfactual Learning NIPS 2015
• Recommendations as Treatments: Debiasing Learning and Evaluation ICML 2016

傾向スコアの推定

まず、傾向スコア$P_{u,i}$がuser independentであると仮定する。これはつまり、$P_{u, i}=P\left(O_{u, i}=1\right)=P\left(O_{*, i}=1\right)=P_{*, i}$。さらに$P_{*, i}=P_{*, i}^{\text {select }} \cdot P_{*, i}^{\text {interact } | \text { select }}$と$P_{*, i}^{\text {interact } | \text { select }}=P_{*, i}^{\text {interact }}$を仮定する。このとき、$P_{*, i}^{\text {interact }}$はuser independentなのでtrue popularity $n_{i}=\sum_{u \in \mathcal{U}} 1\left[i \in \mathcal{S}_{u}\right]$(観測できない)に比例する。

$\hat{P}_{*, i}^{\text {interact }} \propto n_{i}$

一方で$P_{*, i}^{\text {select }}$はべき乗分布を仮定して

$\hat{P}_{*, i}^{\text {select }} \propto\left(n_{i}^{*}\right)^{\gamma}$

このとき$n_{i}^{*}=\sum_{u \in \mathcal{U}, i \in \mathcal{S}_{u}^{*}} O_{*, i}$なのでこっちは観測可能。なので、

$\hat{P}_{*, i} \propto\left(n_{i}^{*}\right)^{\gamma} \cdot n_{i}$

$n_i$が観測できない問題について、$n_i^{*}$が$n_i$でparameterizeされた二項分布$n_{i}^{*} \sim \mathcal{B}\left(n_{i}, P_{*, i}\right)$に従うと仮定すると、

$\hat{P}_{*, i}=\frac{n_{i}^{*}}{n_{i}} \propto\left(n_{i}^{*}\right)^{\gamma} \cdot n_{i}$

となるので

$n_{i} \propto\left(n_{i}^{*}\right)^{\frac{1-\gamma}{2}}$

最終的に、

$\hat{P}_{*, i} \propto\left(n_{i}^{*}\right)^{\left(\frac{\gamma+1}{2}\right)}$

となるので、$\gamma$を推定してやれば良い。$\gamma$の推定については力尽きたので省略。

実験

データセット

• cliteulike

  • Mendeley的なやつ？
  • 論文？を保存するかどうか

• Tradesy

  • ECサイト
  • 商品を買う / 欲しい物リストに入れるかどうか

• Amazon book

  • 本を買うかどうか

比較手法

• Bayesian Personalized Ranking (BPR)
• Collaborative Metric Learning with Uniform Weights (U-CML)
• CML with Approximate-Rank Weights (A-CML)
• Probabilistic Matrix Factorization (PMF)

Popularity biasの調査

interaction bias

• ユーザーは人気アイテムとinteractionしがちである = 偏りがある

presentation bias

• 推薦システム自体が偏りのあるデータから学習しているので人気アイテムを推薦しがち
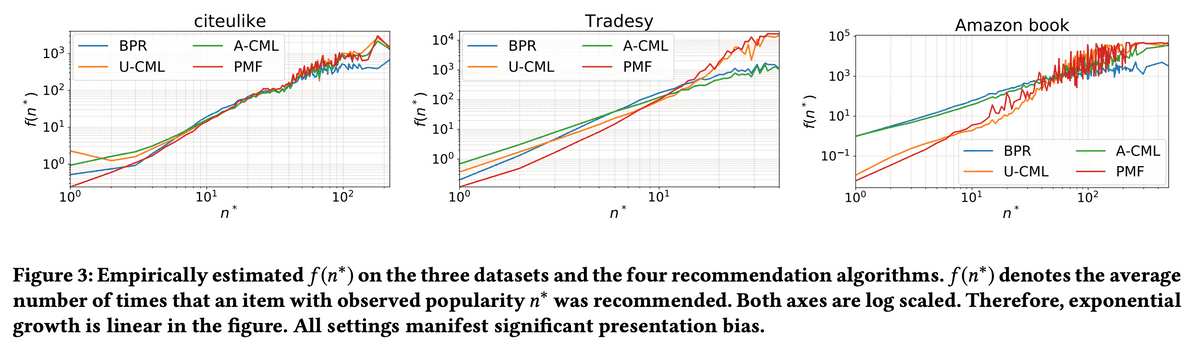
• 横軸はアイテムの観測回数、縦軸は上位50で推薦された回数

Unbiased Evaluatorでの評価結果

• アルゴリズム、データセット、評価尺度にかかわらず(AOAと比べたときに)評価値は下がった。

  • 今までAOA Evaluatorでアルゴリズムが過大評価されていたことの示唆。

バイアス除去の性能評価

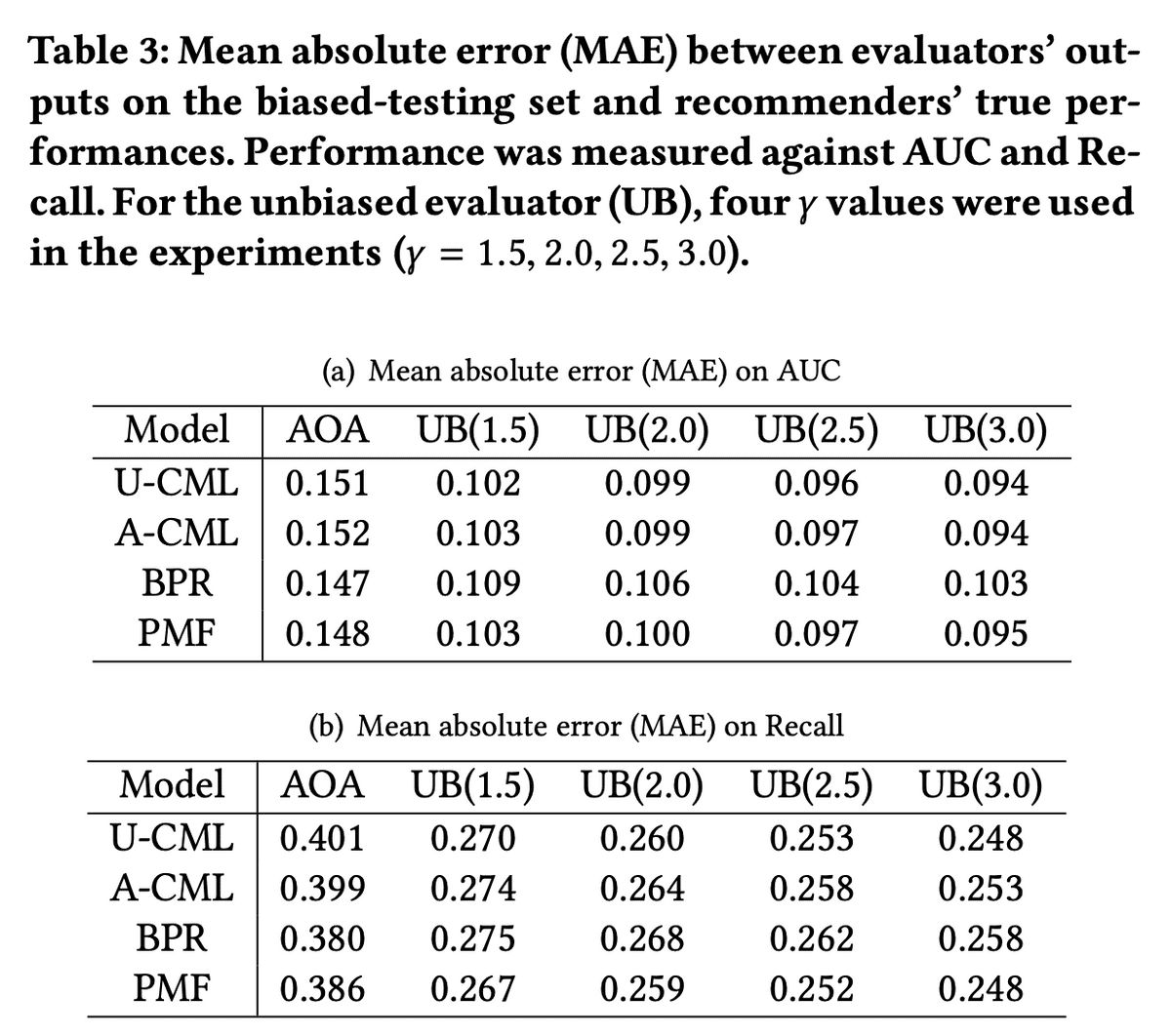
Yahoo! Music rating datasetを使用。このデータセットのテストデータは完全にランダムな推薦によって収集されているところがポイント。このテストデータとは別に訓練データからサンプリングすることで「バイアスありテストデータ」を作成。「(バイアスの無い)テストデータ」と「バイアスありテストデータ」に対する各Evaluatorの値の誤差を比較。

おわりに

人気アイテムは推薦機会とfeedbackの機会が多いので、そうでないアイテムとの差について問題意識をもってlossを設計していきたいな〜