n番煎じ感ありますが、「ガウス過程と機械学習」を読んだのでガウス過程回帰についてメモ。かなり五月雨式ではありますが。。。
ところどころコードも挟んでます。
線形回帰と次元の呪い
1次元の入力xについて
ϕ(x)=(1,x,x2,x3)T
という特徴ベクトルを考えれば
y=w0+w1x+w2x2+w3x3
という線形回帰モデルとして表される。線形回帰については昔書いたのでこちら参照。
これについて一般化(ϕ(x)=(1,x,x2,x3)T)すると
y=wTϕ(x)
先程の式は4つの基底関数の重み付き和として見ることができる。
基底関数をϕh(x)=exp(−σ2(x−μh)2)(ガウス基底関数)としたとき、
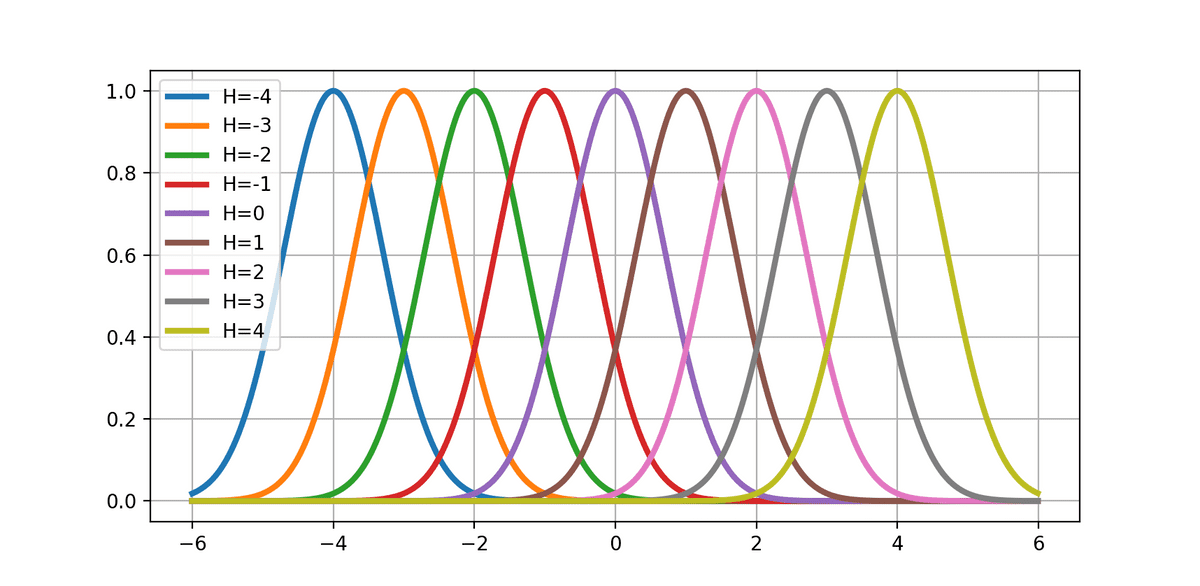
(μh∈(−H,...,−2,−1,0,1,2,...,H))
となる。
import numpy as np
import matplotlib.pyplot as plt
def phi_h(x: float, mu: float, sigma: float) -> float:
return np.exp(- (x - mu) ** 2 / (sigma ** 2))
H: int = 4
for _mu in range(-H, H+1):
x = np.arange(-6, 6, 0.01)
y = np.vectorize(lambda x: phi_h(x, _mu, 1.0))(x)
plt.plot(x, y, label=f"H={_mu}", linewidth=3)
plt.grid()
plt.legend()
plt.show()
先ほどの基底関数に関して適当に重み付けを行い、
y=h=−H∑Hwhexp(−σ2(x−μh)2 )
とすると、下記のようなほとんど任意の形の関数が表される。
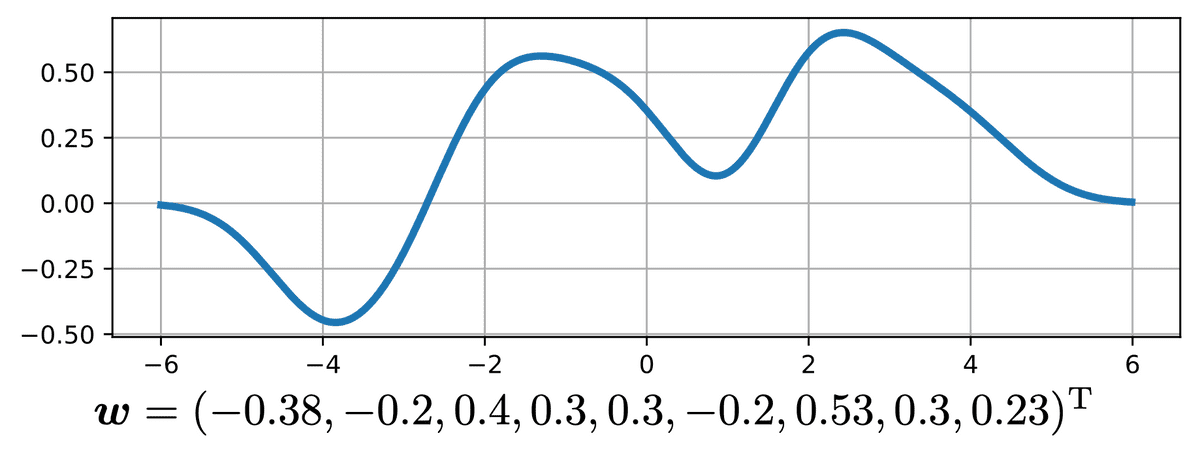 この方法は動径基底関数回帰(radial basis function regression)という。
この方法は動径基底関数回帰(radial basis function regression)という。
import numpy as np
import matplotlib.pyplot as plt
def phi_h(x: float, mu: float, sigma: float) -> float:
return np.exp(- (x - mu) ** 2 / (sigma ** 2))
H: int = 4
x = np.arange(-6, 6, 0.01)
y: np.ndarray = np.zeros_like(x)
mu = range(-H, H+1)
w = [-0.38, -0.2, 0.4, 0.3, 0.3, -0.2, 0.53, 0.3, 0.23]
assert len(mu) == len(w), "ベクトルμとベクトルwの長さが異なります。"
for _mu, _w in zip(mu, w):
y += _w * np.vectorize(lambda x: phi_h(x, _mu, 1.0))(x)
plt.plot(x, y, linewidth=3)
plt.grid()
plt.show()
一見すると任意の関数を表現することができそうなので良さそうだが、入力xが1次元のとき、H=10としたとき重みwの次元は 2H+1=21次元。
これは基底関数の個数と同じ。
入力 x が2次元のとき、基底関数の個数は212=441。
入力 x が3次元のとき、基底関数の個数は213=9261…
入力 x が10次元のとき、基底関数の個数は2110=16679880978201…
これを、次元の呪い(curse of dimensionality)という。
入力 x が2次元、H=1の例
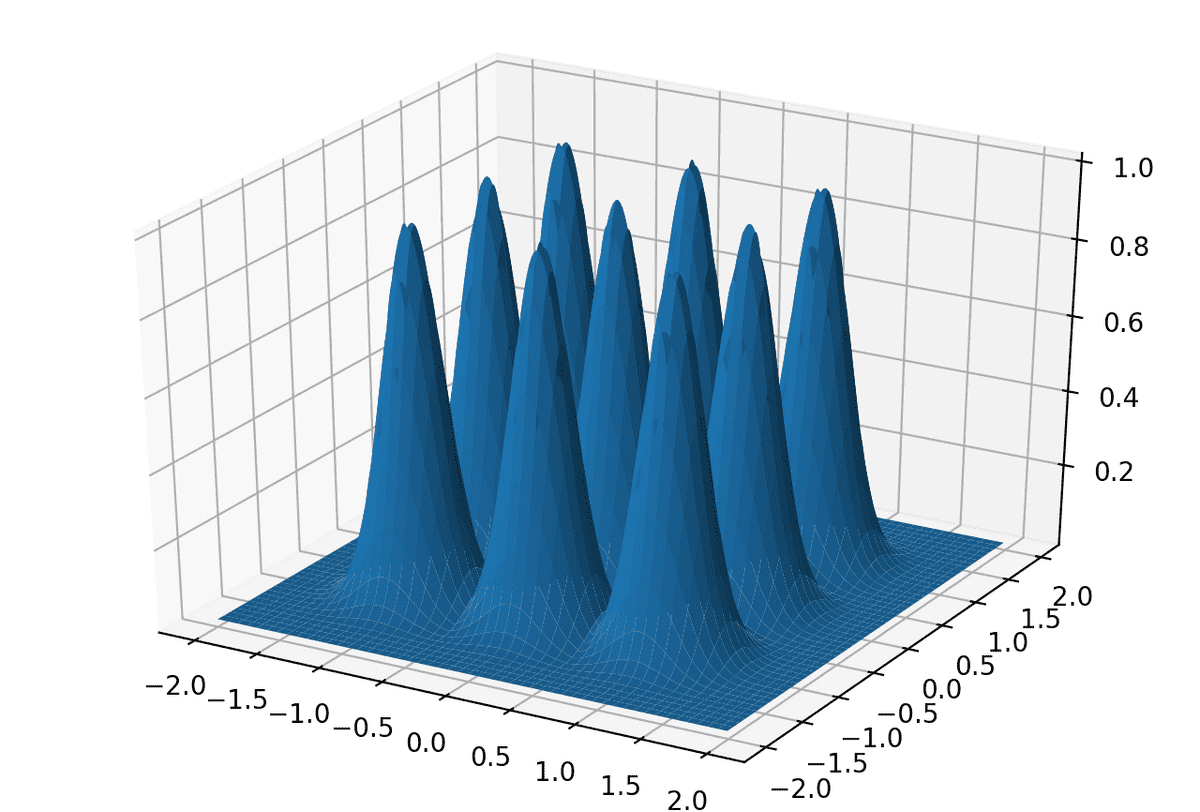
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def phi_h(x: float, mu: float, sigma: float) -> float:
return np.exp(- (x - mu) ** 2 / (sigma ** 2))
H: int = 1
sigma: float = 0.3
x1 = np.arange(-(H+1), (H+1), 0.01)
x2 = np.arange(-(H+1), (H+1), 0.01)
xx1, xx2 = np.meshgrid(x1, x2)
yy = np.zeros_like(xx1)
fig = plt.figure()
ax = Axes3D(fig)
for mu1 in range(-H, H+1):
for mu2 in range(-H, H+1):
yy = np.maximum(yy, np.vectorize(lambda x: phi_h(x, mu1, sigma))(xx1) * np.vectorize(lambda x: phi_h(x, mu2, sigma))(xx2))
ax.plot_surface(xx1, xx2, yy)
plt.show()
ガウス過程
ということで無限次元の基底関数について無限次元の重みwを計算するのは不可能なので、wについて事前分布を設け、w期待値をとって積分消去することを考える。
入力 x について x の特徴ベクトルを
ϕ(x)=(ϕ0(x),ϕ1(x),⋯,ϕH(x))T
とするとN個の特徴ベクトルに対する線形回帰は下記のように表される。
y^⎝⎜⎜⎜⎜⎛ y^1 y^2 ⋮ y^N⎠⎟⎟⎟⎟⎞=Φ⎝⎜⎜⎜⎜⎛ ϕ0(x1) ϕ0(x2) ⋮ ϕ0(xN)ϕ1(x1)ϕ1(x2)⋮ϕ1(xN)⋯⋯⋱⋯ϕH(x1)ϕH(x2)⋮ϕH(xN) ⎠⎟⎟⎟⎟⎞w⎝⎜⎜⎜⎜⎜⎜⎜⎛ w0 w1 ⋮ ⋮ wH⎠⎟⎟⎟⎟⎟⎟⎟⎞
ここで、計画行列Φは x1,⋯xNが与えられれば定数行列となる。
重みがRidge Regressionと同様に w∼N(0,λ2I) に従うとき、
線形変換された y=Φw もまたガウス分布に従う。
このとき、共分散行列は
Σ=E[yyT]− E[y]E[y]T=E[(Φw)(Φw)T] (∵E[y]=E[Φw]=ΦE[w]=0)=ΦE[wwT]ΦT=λ2ΦΦT (∵E[wwT]=λ2I)
となる。したがって、y の分布は多変量ガウス分布
y=N(0,λ2ΦΦT)
となる。上記の式は、線形回帰モデルにあった重み w は期待値が取られて消えていることに注意。
つまり、y の分布はデータ数Nに依存する共分散行列λ2ΦΦTによってきまることになる。
件の共分散行列をK=λ2ΦΦT、x の特徴ベクトルをϕ(x)=(ϕ0(x),ϕ1(x),⋯,ϕH(x))Tとすると、(n,n′)要素は
Knn′=λ2ϕ(xn)Tϕ(xn′)
となる。つまり、2つの変数の共分散が大きいとは、似た値を取りやすいということなので、特徴量ベクトルの内積が大きい、すなわち特徴ベクトル空間において xn と xn が似ているなら、対応するyn、yn も似た値を持つことになる。
K=λ2ΦΦT=λ2Φ⎝⎜⎜⎜⎛ ⋮ϕ(xn)T⋮⎠⎟⎟⎟⎞ΦT( ⋯ϕ(xn′)⋯)
参考書の中には、「ガウス過程の直感的な性質として入力 x が似ていれば、出力 y も似ている」という旨が書かれていましたが、まさしくこのこと言っているのだと感じた。
参考書と同様に観測データ y は予め平均を引いておけば平均を 0 にできるので下記のガウス過程を扱う。
y∼N(0,K)
カーネルトリック
上の式によれば、y の分布は共分散行列 K の要素、
Knn′=λ2ϕ(xn)Tϕ(xn′)
だけで定まることがわかる。この値については結果さえ求まれば、ϕ(xn) を明示的に求める必要はない(!!!!)。
Knn′ の値を与える関数を
xn と xn のカーネル関数(kernel function)とよび
k(xn,xn′)=ϕ(xn)Tϕ(xn′)
と書く。
特徴ベクトルϕ(x)を直接表現することを避け、カーネル関数だけで内積を計算することをカーネルトリック(kernel trick)と呼ぶ。
ガウス過程の定義
Definition 3.4 (ガウス過程の正確な定義)
どんな自然数Nについても、入力 x1,x2,⋯,xN∈X に対応する出力のベクトル
f=(f(x1),f(x2),⋯f(xN))
が平均
μ=(μ(x1),μ(x2),⋯,μ(xN))
と
Knn′=k(xn,xn′)
を要素とする行列Kを共分散行列とするガウス分布 N(μ,K) に従うとき、
f はガウス過程に従うといい、これを
f∼GP(μ(x),k(x,x′))
と書く。
ガウス過程からのサンプル
入力 x の間の類似度を図るためによく使われるガウスカーネル(Gaussian kernel)
k(x,x′)=θ1exp(−θ2∣x−x′∣2)
についてサンプルを行ってみると下記のようなサンプルが得られる。
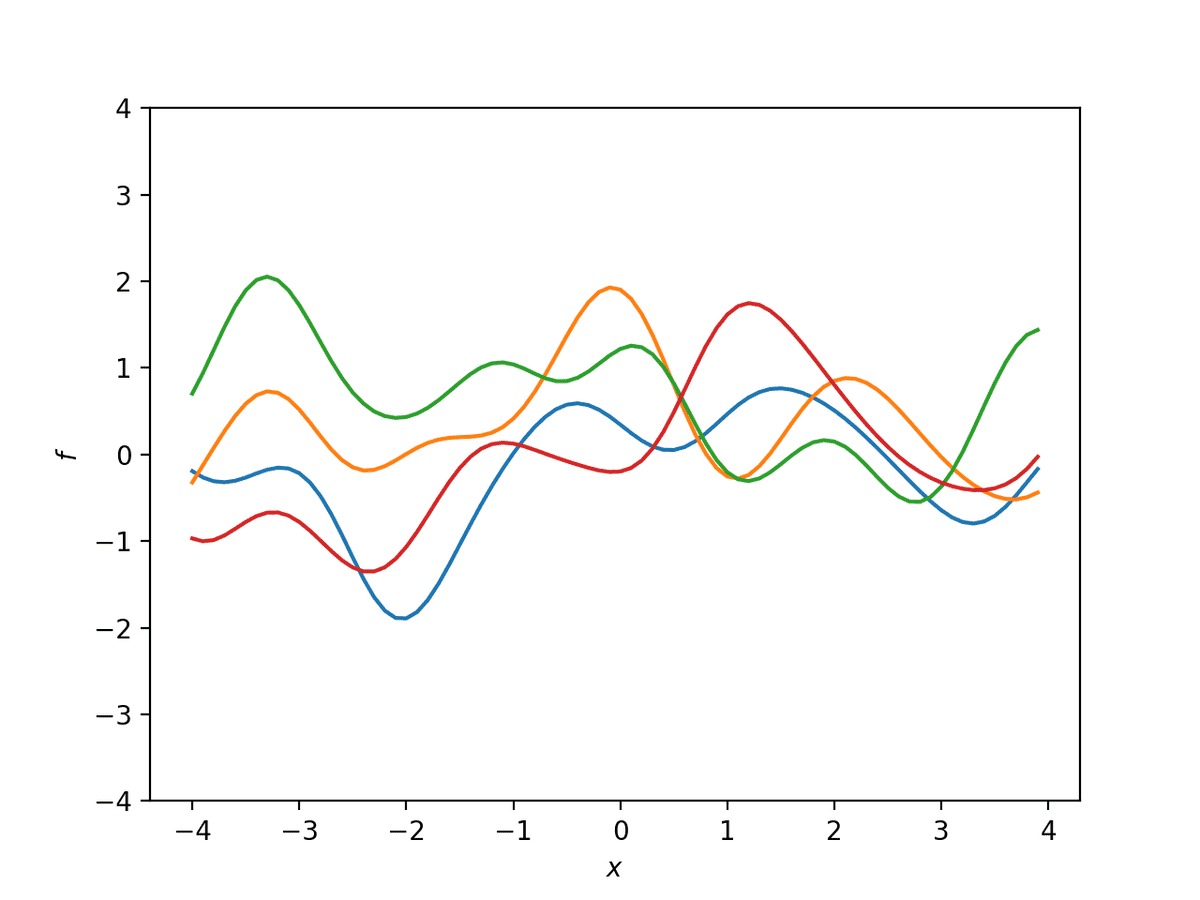 また、このときのKを可視化すると、
また、このときのKを可視化すると、
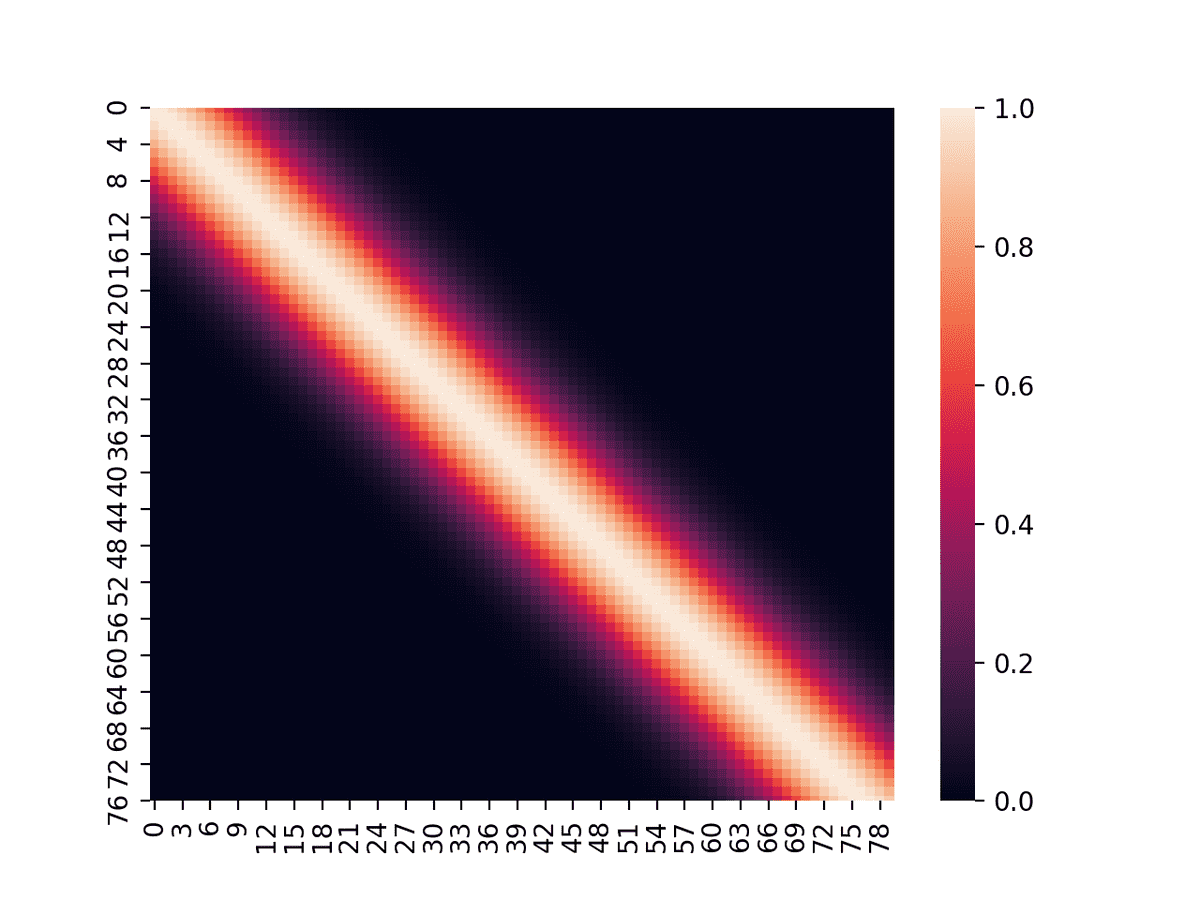 となっており、近いデータ間の共分散が大きくなっていることがわかる。
となっており、近いデータ間の共分散が大きくなっていることがわかる。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
def rbf(x1, x2, theta1=1.0, theta2=1.0):
return theta1 * np.exp(- (x1 - x2)**2 / theta2)
x = np.arange(-4, 4, 0.1)[:, None]
zero = np.zeros(len(x))
K = np.zeros_like(x @ x.T)
for i in range(len(x)):
for j in range(len(x)):
K[i, j] = rbf(x[i], x[j])
for i in range(4):
y = np.random.multivariate_normal(zero, K)
plt.plot(x.flatten(), y)
plt.ylim([-4, 4])
plt.ylabel("$f$")
plt.xlabel("$x$")
plt.show()
print(np.linalg.eigvals(K+0.01+np.eye(len(K))))
sns.heatmap(K)
plt.show()

 この方法は動径基底関数回帰(radial basis function regression)という。
この方法は動径基底関数回帰(radial basis function regression)という。
 また、このときのを可視化すると、
また、このときのを可視化すると、
 となっており、近いデータ間の共分散が大きくなっていることがわかる。
となっており、近いデータ間の共分散が大きくなっていることがわかる。